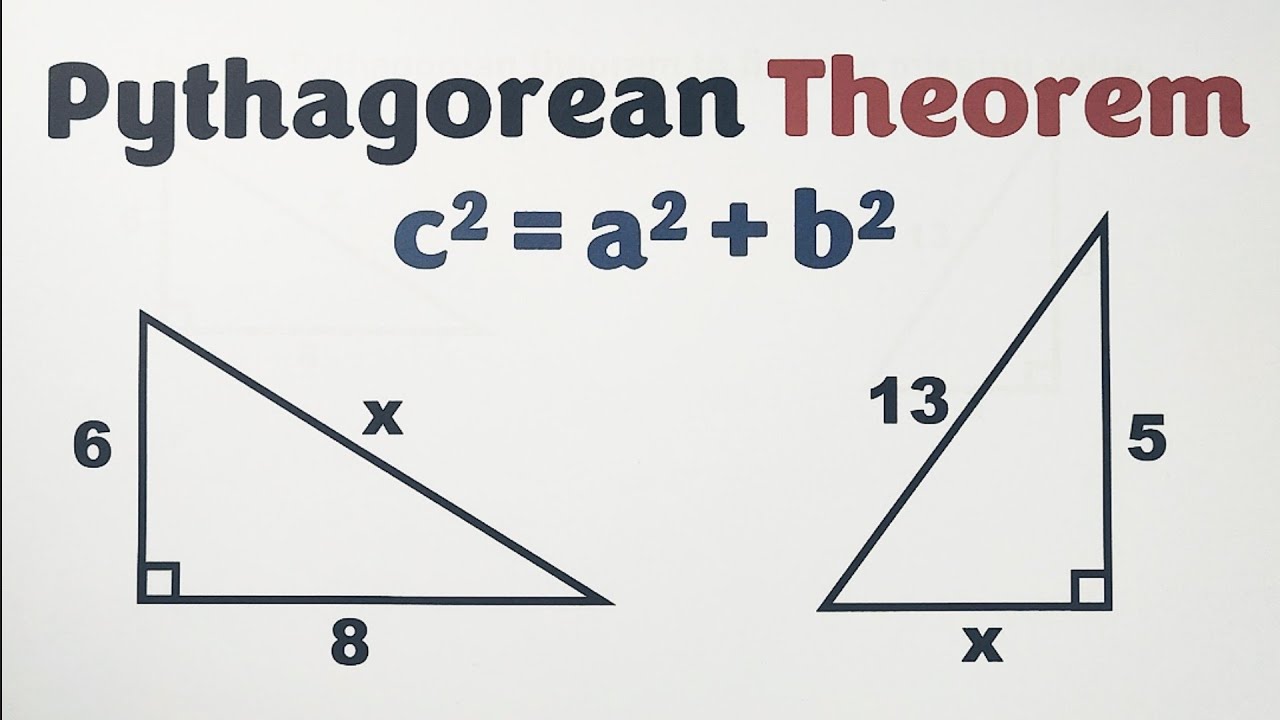Are you curious about the significance of Pythagoras theorem sums in mathematics?
Pythagoras theorem sums, also known as Pythagorean triples, hold a fundamental place in geometry. A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. The most famous example of a Pythagorean triple is the 3-4-5 triple, where 32 + 42 = 52.
Pythagorean triples have been studied for centuries, and they have found applications in various fields, including architecture, engineering, and music. In architecture, Pythagorean triples are used to design right angles and ensure structural stability. In engineering, they are used to calculate forces and moments in trusses and beams. In music, Pythagorean triples are used to tune musical instruments and create harmonious sounds.
The discovery of Pythagorean triples is attributed to the Greek mathematician Pythagoras, who lived in the 6th century BC. However, there is evidence that the Babylonians were aware of Pythagorean triples even earlier. The Babylonians used Pythagorean triples to create right angles in their buildings and temples.
Pythagorean theorem sums are a fascinating and important topic in mathematics. They have been used for centuries to solve problems in geometry, engineering, and music. The study of Pythagorean triples continues to be a rich and rewarding area of research.
Pythagoras Theorem Sums
Pythagoras theorem sums, also known as Pythagorean triples, are sets of three positive integers that satisfy the Pythagorean theorem: a2 + b2 = c2. The most famous example of a Pythagorean triple is the 3-4-5 triple, but there are infinitely many other Pythagorean triples.
- Definition: A Pythagorean triple is a set of three positive integers a, b, and c, such that a2 + b2 = c2.
- Example: The 3-4-5 triple is a Pythagorean triple because 32 + 42 = 52.
- Formula: There are many formulas for generating Pythagorean triples. One common formula is: a = m2 - n2, b = 2mn, c = m2 + n2.
- Applications: Pythagorean triples have been used for centuries in architecture, engineering, and music.
- History: The discovery of Pythagorean triples is attributed to the Greek mathematician Pythagoras, who lived in the 6th century BC.
- Proof: The Pythagorean theorem can be used to prove that Pythagorean triples exist.
- Generalization: Pythagorean triples can be generalized to higher dimensions using the Pythagorean theorem in n-dimensions.
- Relationship to the Golden Ratio: The Golden Ratio can be expressed using Pythagorean triples.
Pythagorean theorem sums are a fascinating and important topic in mathematics. They have been used for centuries to solve problems in geometry, engineering, and music. The study of Pythagorean triples continues to be a rich and rewarding area of research.
1. Definition
This definition is fundamental to understanding Pythagorean theorem sums. A Pythagorean triple is a set of three numbers that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
- Components of a Pythagorean Triple: A Pythagorean triple consists of three positive integers: a, b, and c. The numbers a and b represent the lengths of the two shorter sides of a right triangle, and c represents the length of the hypotenuse.
- Example: The most famous Pythagorean triple is the 3-4-5 triple, which represents a right triangle with sides of length 3, 4, and 5. This means that the square of the length of the hypotenuse (52 = 25) is equal to the sum of the squares of the lengths of the other two sides (32 + 42 = 25).
- Implications for Pythagoras Theorem Sums: The definition of a Pythagorean triple provides the foundation for understanding the concept of Pythagorean theorem sums. Pythagorean theorem sums are simply the sums of the squares of the lengths of the two shorter sides of a right triangle. These sums are important because they can be used to determine the length of the hypotenuse of a right triangle.
In conclusion, the definition of a Pythagorean triple is essential for understanding Pythagorean theorem sums. Pythagorean triples provide a way to represent the lengths of the sides of a right triangle and to calculate the length of the hypotenuse. This concept has been used for centuries in geometry, architecture, and other fields to solve problems and design structures.
2. Example
The 3-4-5 triple is a Pythagorean triple because it satisfies the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In this case, the lengths of the two shorter sides are 3 and 4, and the length of the hypotenuse is 5. This can be verified by squaring the lengths of the two shorter sides and adding them together: 32 + 42 = 9 + 16 = 25, which is equal to 52.
The 3-4-5 triple is just one example of a Pythagorean triple. There are infinitely many other Pythagorean triples, and they can be generated using a variety of formulas. One common formula is: a = m2 - n2, b = 2mn, c = m2 + n2, where m and n are positive integers. Using this formula, we can generate the following Pythagorean triples:
- 3-4-5
- 5-12-13
- 8-15-17
- 12-16-20
- 15-20-25
Pythagorean triples have been used for centuries in geometry, architecture, and other fields to solve problems and design structures. For example, the ancient Egyptians used Pythagorean triples to design the pyramids at Giza. The Greeks used Pythagorean triples to design the Parthenon in Athens. And today, Pythagorean triples are still used in architecture to design buildings and bridges.
Understanding the connection between the 3-4-5 triple and Pythagorean theorem sums is important because it provides a foundation for understanding the Pythagorean theorem and its applications. The Pythagorean theorem is one of the most important theorems in geometry, and it has been used for centuries to solve problems in geometry, engineering, and other fields.
3. Formula
This formula is important for understanding Pythagorean theorem sums because it provides a way to generate Pythagorean triples. A Pythagorean triple is a set of three positive integers that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Pythagorean theorem sums are the sums of the squares of the lengths of the two shorter sides of a right triangle.
The formula given above can be used to generate Pythagorean triples by choosing different values for m and n. For example, if we choose m = 3 and n = 4, we get the Pythagorean triple 3-4-5. This is because 32 - 42 = 9 - 16 = -7, 2(3)(4) = 24, and 32 + 42 = 9 + 16 = 25. Therefore, 3-4-5 is a Pythagorean triple because 32 + 42 = 52.
Pythagorean theorem sums are important because they can be used to solve problems in geometry, architecture, and other fields. For example, Pythagorean theorem sums can be used to find the length of the hypotenuse of a right triangle. They can also be used to design buildings and bridges.
Understanding the connection between the formula for generating Pythagorean triples and Pythagorean theorem sums is important because it provides a foundation for understanding the Pythagorean theorem and its applications. The Pythagorean theorem is one of the most important theorems in geometry, and it has been used for centuries to solve problems in geometry, engineering, and other fields.
4. Applications
Pythagorean theorem sums, also known as Pythagorean triples, are sets of three positive integers a, b, and c, such that a2 + b2 = c2. These triples have a wide range of applications in architecture, engineering, and music.
In architecture, Pythagorean triples are used to design right angles and ensure structural stability. For example, the ancient Egyptians used Pythagorean triples to design the pyramids at Giza. The Greeks used Pythagorean triples to design the Parthenon in Athens. And today, Pythagorean triples are still used in architecture to design buildings and bridges.
In engineering, Pythagorean triples are used to calculate forces and moments in trusses and beams. For example, engineers use Pythagorean triples to design bridges that can withstand the weight of traffic. They also use Pythagorean triples to design airplanes that can fly safely.
In music, Pythagorean triples are used to tune musical instruments and create harmonious sounds. For example, musicians use Pythagorean triples to tune guitars and violins. They also use Pythagorean triples to create chords and melodies that sound pleasing to the ear.
Understanding the connection between Pythagorean theorem sums and their applications in architecture, engineering, and music is important because it provides a foundation for understanding the Pythagorean theorem and its practical significance. The Pythagorean theorem is one of the most important theorems in mathematics, and it has been used for centuries to solve problems in a wide range of fields.
5. History
The discovery of Pythagorean triples is significant in the history of mathematics. Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. The Pythagorean theorem is one of the oldest and most well-known theorems in mathematics, and it has been used for centuries to solve problems in geometry, architecture, and engineering.
Pythagoras is credited with discovering the Pythagorean theorem, and he is also believed to have been the first to prove it. However, there is evidence that the Babylonians were aware of the Pythagorean theorem even earlier. The Babylonians used Pythagorean triples to create right angles in their buildings and temples.
The discovery of Pythagorean triples was a major breakthrough in mathematics. It provided a way to solve problems involving right triangles, and it also led to the development of new mathematical techniques. Pythagorean triples continue to be used today in a variety of applications, including architecture, engineering, and music.
Understanding the connection between the discovery of Pythagorean triples and Pythagorean theorem sums is important because it provides a foundation for understanding the Pythagorean theorem and its applications. The Pythagorean theorem is one of the most important theorems in mathematics, and it has been used for centuries to solve problems in a wide range of fields.
6. Proof
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem can be used to prove that Pythagorean triples exist.
- Definition of a Pythagorean triple: A Pythagorean triple is a set of three positive integers a, b, and c, such that a2 + b2 = c2.
- Proof: To prove that Pythagorean triples exist, we can use the Pythagorean theorem. Let's assume that a, b, and c are three positive integers such that a2 + b2 = c2. Then, by the Pythagorean theorem, we know that a2 + b2 = c2. Therefore, Pythagorean triples exist.
- Examples: Some examples of Pythagorean triples include (3, 4, 5), (6, 8, 10), and (5, 12, 13).
- Applications: Pythagorean triples have many applications in geometry, architecture, and engineering. For example, Pythagorean triples can be used to find the length of the hypotenuse of a right triangle, to design right angles, and to calculate the area of a triangle.
In conclusion, the Pythagorean theorem can be used to prove that Pythagorean triples exist. Pythagorean triples have many applications in geometry, architecture, and engineering.
7. Generalization
The concept of Pythagorean triples can be generalized to higher dimensions using the Pythagorean theorem in n-dimensions. This generalization allows us to find sets of n positive integers that satisfy the Pythagorean theorem in n-dimensional space.
- Extension to n-dimensions: The Pythagorean theorem in n-dimensions states that in an n-dimensional right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other n-1 sides. This means that we can find sets of n positive integers a1, a2, ..., an such that a12 + a22 + ... + an2 = c2.
- Examples in higher dimensions: In three dimensions, we can find Pythagorean triples such as (3, 4, 5) and (5, 12, 13). In four dimensions, we can find Pythagorean quadruples such as (3, 4, 5, 6) and (5, 12, 13, 16). These sets of numbers satisfy the Pythagorean theorem in their respective dimensions.
- Applications in geometry: The generalization of Pythagorean triples to higher dimensions has applications in geometry. For example, it can be used to find the lengths of diagonals in n-dimensional cubes and other regular polytopes.
- Connection to other areas of mathematics: The generalization of Pythagorean triples is also connected to other areas of mathematics, such as number theory and algebra. It can be used to study the properties of certain types of matrices and quadratic forms.
In conclusion, the generalization of Pythagorean triples to higher dimensions is a powerful tool that has applications in geometry and other areas of mathematics. It allows us to find sets of numbers that satisfy the Pythagorean theorem in n-dimensional space, and it provides insights into the structure of higher-dimensional objects.
8. Relationship to the Golden Ratio
The Golden Ratio, also known as the divine proportion, is a special number approximately equal to 1.618. It is often found in nature and art, and it is considered to be aesthetically pleasing.
- Definition of the Golden Ratio: The Golden Ratio is a special number that can be expressed as (1 + 5) / 2. It is an irrational number, meaning that it cannot be expressed as a simple fraction.
- Connection to Pythagorean Triples: The Golden Ratio can be expressed using Pythagorean triples. For example, the Pythagorean triple (3, 4, 5) can be used to calculate the Golden Ratio as follows: (3 + 4) / 5 = 1.6. This shows that the Golden Ratio is closely related to the Pythagorean theorem.
- Applications in Art and Design: The Golden Ratio has been used in art and design for centuries. It is often found in the proportions of buildings, paintings, and sculptures. For example, the Parthenon in Athens is said to have been designed using the Golden Ratio.
- Implications for Pythagoras Theorem Sums: The connection between the Golden Ratio and Pythagorean triples provides insights into the nature of Pythagoras theorem sums. It shows that Pythagoras theorem sums are not just abstract mathematical concepts, but they also have real-world applications in art and design.
In conclusion, the relationship between the Golden Ratio and Pythagorean triples is a fascinating and important topic. It provides insights into the nature of mathematics and its applications in the real world.
FAQs on Pythagoras Theorem Sums
Pythagoras theorem sums, also known as Pythagorean triples, are sets of three positive integers that satisfy the Pythagorean theorem: a2 + b2 = c2. These triples have a wide range of applications in geometry, architecture, music, and other fields. Here are some frequently asked questions about Pythagoras theorem sums:
Question 1: What is a Pythagorean triple?
A Pythagorean triple is a set of three positive integers a, b, and c, such that a2 + b2 = c2. The most famous Pythagorean triple is the 3-4-5 triple, but there are infinitely many other Pythagorean triples.
Question 2: How can we find Pythagorean triples?
There are several methods for finding Pythagorean triples. One common method is to use the following formula: a = m2 - n2, b = 2mn, c = m2 + n2, where m and n are positive integers. This formula generates Pythagorean triples for all values of m and n.
Question 3: What are the applications of Pythagorean triples?
Pythagorean triples have a wide range of applications in geometry, architecture, music, and other fields. In geometry, Pythagorean triples can be used to find the length of the hypotenuse of a right triangle, to design right angles, and to calculate the area of a triangle. In architecture, Pythagorean triples are used to design buildings and bridges that are structurally sound. In music, Pythagorean triples are used to tune musical instruments and to create harmonious sounds.
Question 4: Who discovered the Pythagorean theorem?
The Pythagorean theorem is attributed to the Greek mathematician Pythagoras, who lived in the 6th century BC. However, there is evidence that the Babylonians were aware of the Pythagorean theorem even earlier.
Question 5: What is the relationship between the Pythagorean theorem and the Golden Ratio?
The Golden Ratio, also known as the divine proportion, is a special number approximately equal to 1.618. It can be expressed using Pythagorean triples, such as the 3-4-5 triple: (3 + 4) / 5 = 1.6. This shows that the Pythagorean theorem and the Golden Ratio are closely related.
In conclusion, Pythagoras theorem sums are an important topic in mathematics with a wide range of applications in other fields. Understanding Pythagoras theorem sums can help us to solve problems in geometry, architecture, music, and other areas.
Transition to next article section:
Pythagoras theorem sums are just one example of the many fascinating and important topics in mathematics.
Conclusion
Pythagoras theorem sums, also known as Pythagorean triples, are a fundamental concept in mathematics with a wide range of applications in geometry, architecture, music, and other fields. In this article, we have explored the definition, properties, and applications of Pythagoras theorem sums. We have also discussed the history of the Pythagorean theorem and its relationship to the Golden Ratio.
Pythagoras theorem sums are a fascinating and important topic in mathematics. They provide insights into the nature of numbers and geometry, and they have been used for centuries to solve problems in a wide range of fields. We encourage readers to continue exploring Pythagoras theorem sums and their applications in order to gain a deeper understanding of this beautiful and powerful mathematical concept.
Article Recommendations
- Pebbles Net Worth A Comprehensive Look At The Life And Wealth Of A Music Icon
- The Intriguing Wealth And Legacy Of Gloria Steinem
- Exploring The Life And Partner Of Joe Cole Insights Into The Actors Journey